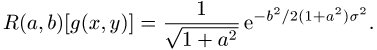Trasformata di Radon

In matematica, la trasformata di Radon è la trasformata integrale che porta una funzione f definita sul piano a una funzione Rf definita sullo spazio (bidimensionale) delle rette del piano, il cui valore su una particolare retta è uguale all'integrale della funzione su quella retta. La trasformata fu introdotta nel 1917 da Johann Radon, che fornì anche una formula per la trasformata inversa, l'antitrasformata di Radon; Radon incluse anche formule per la trasformata in tre dimensioni, in cui l'integrale è preso sui piani (l'integrazione sulle linee è nota come trasformata dei raggi X). In seguito è stata generalizzata a spazi euclidei di dimensioni superiori e, più in generale, nel contesto della geometria integrale. L'analogo complesso della trasformata di Radon è noto come trasformata di Penrose. La trasformata di Radon è ampiamente applicabile alla tomografia, la creazione di un'immagine a partire dai dati di proiezione associati alle scansioni trasversali di un oggetto, come per esempio nella tomografia assiale computerizzata (TAC).

Significato

Se una funzione ${\displaystyle f}$ rappresenta una densità sconosciuta, la trasformata di Radon rappresenta la proiezione dei dati come risultato di un'analisi tomografica; l'inversa della trasformata di Radon può essere utilizzata per ricostruire la densità originale dai dati proiettati, e quindi costituisce la base matematica della ricostruzione tomografica.

La trasformata di Radon è talvolta detta sinogramma, poiché la trasformata di Radon di una fonte puntiforme non centrata è una sinusoide; di conseguenza, la trasformata di Radon di un certo numero di oggetti piccoli appare graficamente come un certo numero di sinusodi sfocate con ampiezze e fasi differenti.

La trasformata di Radon è utile nella tomografia computerizzata (TC), negli scanner di codici a barre, nella microscopia elettronica di assemblaggi macromolecolari come virus e complessi proteici, nella sismica a riflessione e nella soluzione di equazioni differenziali parziali iperboliche.

Definizione

La trasformata di Radon R della funzione f(x,y) è definita come:

${\displaystyle {\mathcal {R}}_{\theta }(\rho )[f(x,y)]=\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }f(x,y)\delta (\rho -x\cos \theta -y\sin \theta )dxdy}$

dove ${\displaystyle \theta }$ è la pendenza angolare della retta di scansione.

L'antitrasformata di Radon è:

${\displaystyle [f(x,y)]={\frac {1}{2\pi }}\int _{-\infty }^{\infty }{\frac {d}{dy}}{\mathcal {H}}[{\mathcal {U}}(m,y-mx)]dm}$

dove H è la trasformata di Hilbert.

Questa trasformata venne introdotta (per problemi in due e tre dimensioni) nel 1917 dal matematico Johann Radon, che pubblicò anche le formule per il calcolo dell'antitrasformata (problema della ricostruzione), ed è stata in seguito generalizzata al caso di problemi a più dimensioni, nel campo della geometria integrale.

Algoritmo di retroproiezione filtrata

Conoscere la trasformata di Radon di un oggetto permette di ricostruirne la struttura: il teorema della proiezione infatti assicura che se abbiamo un numero infinito di proiezioni monodimensionali di un oggetto fatte da un numero infinito di angoli diversi (ossia: se conosciamo U(m, q) ), possiamo ricostruire perfettamente la geometria dell'oggetto originale (ossia: f(x, y) ) e il processo di ricostruzione consiste appunto nel calcolare l'antitrasformata di Radon.

Tuttavia l'antitrasformata di Radon è molto instabile se i dati misurati sono affetti da rumore sperimentale. Nella pratica si usa perciò una versione stabilizzata e discretizzata dell'antitrasformata di Radon, detta «algoritmo di retroproiezione filtrata». Un corollario al teorema della proiezione afferma infatti che «la trasformata di Radon della convoluzione bidimensionale di due funzioni è uguale alla convoluzione monodimensionale delle loro trasformate di Radon». Conseguenza pratica di ciò è che per eliminare il rumore che riduce la qualità della ricostruzione non è necessario eliminarlo fisicamente alla fonte, ma è possibile filtrare matematicamente i risultati sperimentali (ossia la misura della trasformata di Radon) e quindi operare la ricostruzione (ossia calcolare l'antitrasformata) direttamente sui dati filtrati a posteriori.

Note

Bibliografia

• Deans, Stanley R. (1983). The Radon Transform and Some of Its Applications. New York: John Wiley & Sons.
• Frank Natterer, The Mathematics of Computerized Tomography (Classics in Applied Mathematics, 32), Society for Industrial and Applied Mathematics. ISBN 0898714931
• Frank Natterer and Frank Wubbeling, Mathematical Methods in Image Reconstruction, Society for Industrial and Applied Mathematics. ISBN 0898714729

Voci correlate

• Trasformata Mojette
• Teorema della proiezione

Altri progetti

• Wikimedia Commons contiene immagini o altri file su trasformata di Radon

Collegamenti esterni

• (EN) "Radon Transform" di Eric W. Weisstein (da MathWorld)
• Algoritmo di individuazione di navi tramite trasformata di Radon (per individuazione di petroliere che scaricano illegalmente nel Mar Mediterraneo)
• [1] applett che calcola la trasformata di Radon e la antitrasformata